5.3 The Fundamental Theorem of Calculus, Part I
The FTC was first stated clearly by Isaac Newton in 1666, although other mathematicians, including Newton’s teacher Isaac Barrow, had discovered versions of it earlier.
The Fundamental Theorem of Calculus (FTC) reveals an unexpected connection between the two main operations of calculus: differentiation and integration. The theorem has two parts. Although they are closely related, we discuss them in separate sections to emphasize the different ways they are used.
To explain FTC I, recall a result from Example 5 of Section 5.2:
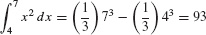
 REMINDER
REMINDER
F(x) is called an antiderivative of f(x) if F′(x) = f(x). We say also that F(x) is an indefinite integral of f(x), and we use the notation
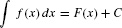
Now observe that 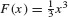 is an antiderivative of x2, so we can write
is an antiderivative of x2, so we can write
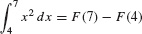
According to FTC I, this is no coincidence; this relation between the definite integral and the antiderivative holds in general.
310
THEOREM 1 The Fundamental Theorem of Calculus, Part I
Assume that f(x) is continuous on [a, b]. If f(x) is an antiderivative of f(x) on [a, b], then
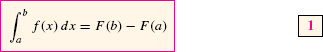
Proof
The quantity F(b) −F(a) is the total change in F (also called the “net change”) over the interval [a, b]. Our task is to relate it to the integral of F′(x) = f(x). There are two main steps.
Step 1. Write total change as a sum of small changes.
Given any partition P of [a, b]:
P : x0 = a < x1 < x2 < ⋯ < xN = b
we can break up F(b) −F(a) as a sum of changes over the intervals [x[em]i[/em]−1, xi]:
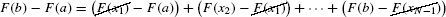
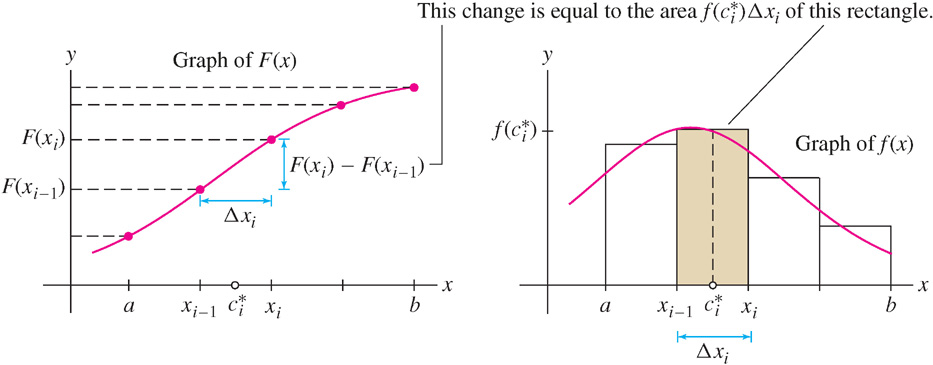
On the right-hand side, F(x1) is canceled by −F(x1) in the second term, F(x2) is canceled by −F(x2), etc. (Figure 1). In summation notation,
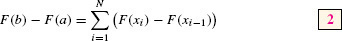
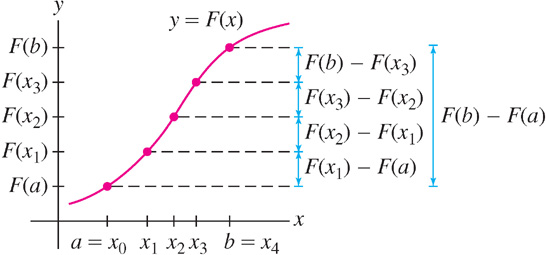
Step 2. Interpret Eq. (2) as a Riemann sum.
The Mean Value Theorem tells us that there is a point 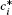 in [x[em]i[/em]−1, xi] such that
in [x[em]i[/em]−1, xi] such that
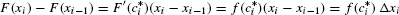
Therefore, Eq. (2) can be written
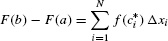
This sum is the Riemann sum R(f, P, C*) with sample points 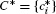 .
.
Now, f(x) is integrable (Theorem 1, Section 5.2), so R(f, P, C*) approaches 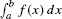 as the norm ‖P‖ tends to zero. On the other hand, R(f, P, C*) is equal to F(b) − F(a) with our particular choice C* of sample points. This proves the desired result:
as the norm ‖P‖ tends to zero. On the other hand, R(f, P, C*) is equal to F(b) − F(a) with our particular choice C* of sample points. This proves the desired result:
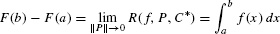
311
CONCEPTUAL INSIGHT A Tale of Two Graphs
In the proof of FTC I, we used the MVT to write a small change in F(x) in terms of the derivative F′(x) = f(x):
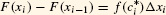
But 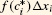 is the area of a thin rectangle that approximates a sliver of area under the graph of f(x) (Figure 2). This is the essence of the Fundamental Theorem: the total change F(b) −F(a) is equal to the sum of small changes F(xi) −F(x[em]i[/em]−1), which in turn is equal to the sum of the areas of rectangles in a Riemann sum approximation for f(x). We derive the Fundamental Theorem itself by taking the limit as the width of the rectangles tends to zero.
is the area of a thin rectangle that approximates a sliver of area under the graph of f(x) (Figure 2). This is the essence of the Fundamental Theorem: the total change F(b) −F(a) is equal to the sum of small changes F(xi) −F(x[em]i[/em]−1), which in turn is equal to the sum of the areas of rectangles in a Riemann sum approximation for f(x). We derive the Fundamental Theorem itself by taking the limit as the width of the rectangles tends to zero.
FTC I tells us that if we can find an antiderivative of f(x), then we can compute the definite integral easily, without calculating any limits. It is for this reason that we use the integral sign ∫ for both the definite integral 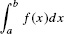 and the indefinite integral (antiderivative) ∫ f(x)dx.
and the indefinite integral (antiderivative) ∫ f(x)dx.
Notation
F(b) −F(a) is denoted 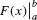 . In this notation, the FTC reads
. In this notation, the FTC reads
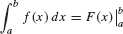
 REMINDER The Power Rule for Integrals (valid for n ≠ −1) states:
REMINDER The Power Rule for Integrals (valid for n ≠ −1) states:
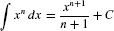
EXAMPLE 1
Calculate the area under the graph of f(x) = x3 over [2, 4].
Solution Since 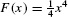 is an antiderivative of f(x) = x3, FTC I gives us
is an antiderivative of f(x) = x3, FTC I gives us
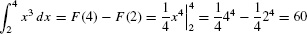
EXAMPLE 2
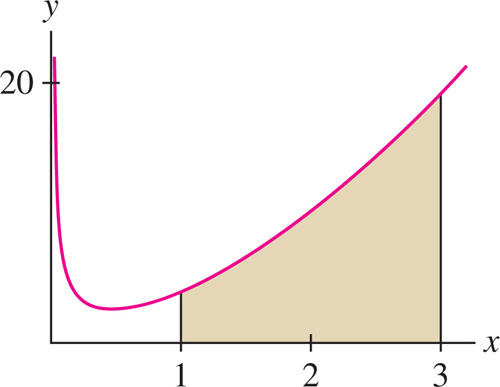
Find the area under g(x) = x−3/4 + 3x5/3 over [1, 3]
Solution The function 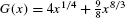 is an antiderivative of g(x). The area (Figure 3) is equal to
is an antiderivative of g(x). The area (Figure 3) is equal to
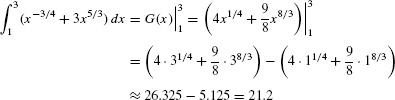
312
EXAMPLE 3
Calculate 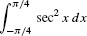 and sketch the corresponding region.
and sketch the corresponding region.
Solution Figure 4 shows the region. Recall that (tan x)′ = sec2x. Therefore,
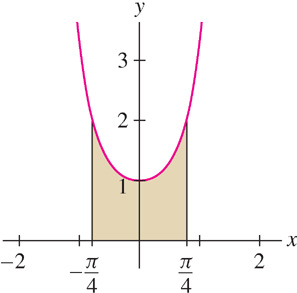
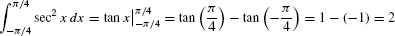
We know that the definite integral is equal to the signed area between the graph and the x-axis. Needless to say, the FTC “knows” this also: When you evaluate an integral using the FTC, you obtain the signed area.
EXAMPLE 4
Evaluate
- (a)
and
- (b)
 .
.
Solution
- (a) Since (−cos x)′ = sin x, the area of one “hump” (Figure 5) is
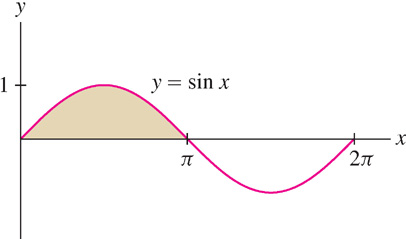 Figure 5.32: The area of one hump is 2. The signed area over [0, 2π] is zero.
Figure 5.32: The area of one hump is 2. The signed area over [0, 2π] is zero.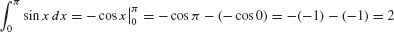
- (b) We expect the signed area over [0, 2π] to be zero since the second hump lies below the x-axis, and, indeed,
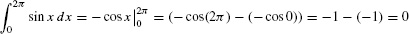
EXAMPLE 5
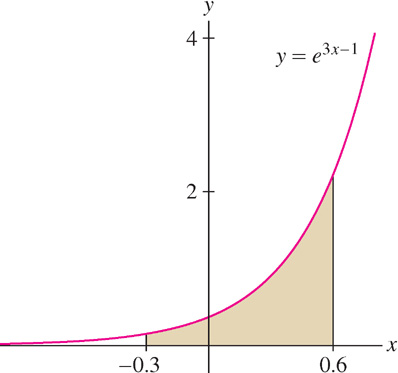
Evaluate 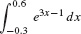 .
.
Solution The function 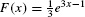 is an antiderivative of f(x) = e3[em]x[/em]−1, so the definite integral (the shaded area in Figure 6) is
is an antiderivative of f(x) = e3[em]x[/em]−1, so the definite integral (the shaded area in Figure 6) is
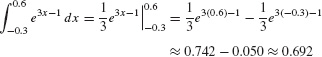
Recall (Section 4.9) that F(x) = ln |x| is an antiderivative of f(x) = x−1 in the domain {x : x ≠ 0}. Therefore, the FTC yields the following formula [Figure 7(A)], which is valid if both a and b are positive or both are negative.
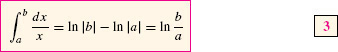
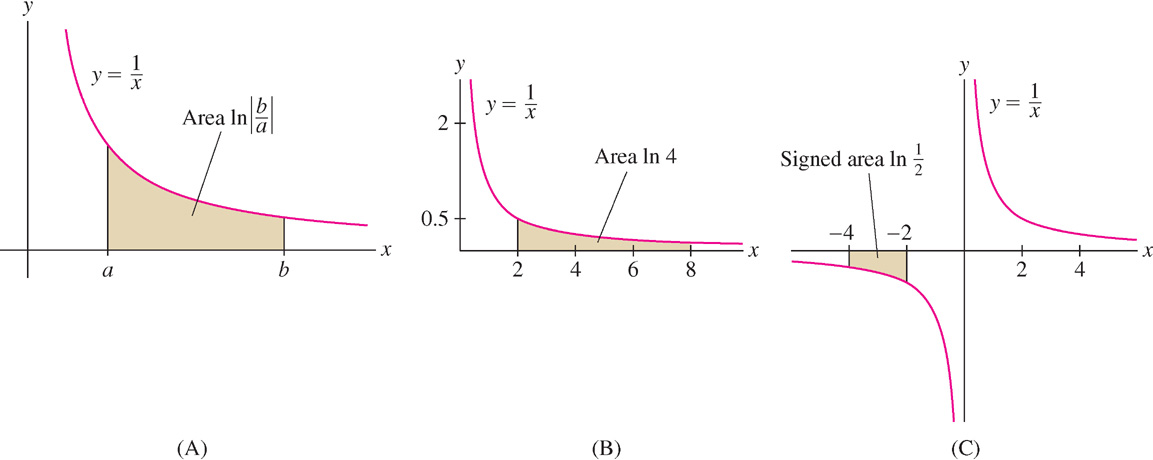
EXAMPLE 6 The Logarithm as an Antiderivative
Evaluate
- (a)
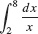
and - (b)
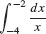 .
.
Solution By Eq. (3),
- (a)
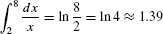
- (b)
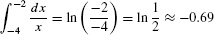
The areas represented by these integrals is shown in Figures 7(B) and (C).
313
CONCEPTUAL INSIGHT Which Antiderivative?
Antiderivatives are unique only to within an additive constant (Section 4.9). Does it matter which antiderivative is used in the FTC? The answer is no. If F(x) and G(x) are both antiderivatives of f(x), then F(x) = G(x) + C for some constant C, and
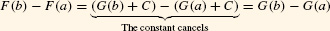
The two antiderivatives yield the same value for the definite integral:
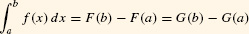
5.3.1 Summary
- The Fundamental Theorem of Calculus, Part I, states that
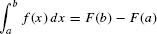
where F(x) is an antiderivative of f(x). FTC I is used to evaluate definite integrals in cases where we can find an antiderivative of the integrand. - Basic antiderivative formulas for evaluating definite integrals:
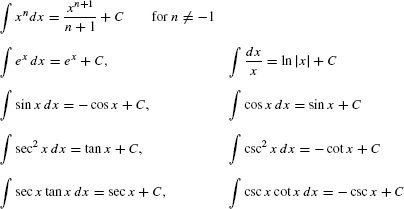
314